O ASSASSINATO PARA OCULTAR UMA DESCVOBERTA MATEMÁTICA "PERIGOSA"
O assassinato cometido para ocultar uma descoberta matemática 'perigosa'

Dizem que certa manhã, em meados do século VI a.C., um homem foi jogado em mar aberto no litoral da Grécia.
Seu nome era Hipaso de Metaponto, matemático, teórico da música e filósofo pré-socrático.
Ele foi abandonado à sua própria sorte - e ela não poderia ser outra senão sua morte.
Como freqüentemente acontece com o que conhecemos sobre o mundo antigo, há aqueles que acreditam que isso aconteceu, enquanto outros questionam essa versão.
Ninguém ainda foi capaz de verificar se essa parte da história é verdadeira.
Mas a outra parte dela é a mais interessante: a razão pela qual eles queriam matá-lo.
E é que poucos assassinatos têm um motivo tão assombroso quanto a descoberta da incomensurabilidade e da irracionalidade, matematicamente falando.
- As tabelas trigonométricas mais fáceis e precisas, criadas mil anos antes de Pitágoras
- Algumas perguntas que você teria que responder para ser aceito na Mensa, organização para superdotados
- As manias esquisitas de Einstein que podem nos ensinar lições úteis
 GETTY IMAGES
GETTY IMAGESUma estrela da antiguidade
A história tem início com uma das celebridades da Grécia antiga, Pitágoras de Samos (c. 580-c. 500 aC), o criador do famoso teorema que você deve ter aprendido na escola.
Pitágoras é, na verdade, um personagem controverso. Como ele não deixou nada por escrito, muitos se perguntaram se ele realmente foi o autor de muitas das descobertas revolucionárias no campo da matemática que lhe foram atribuídas.
A única prova é de que ele fundou uma escola, embora seus ensinamentos fossem considerados suspeitos e seus seguidores, estranhos.
 GETTY IMAGES
GETTY IMAGESOs pitagóricos
As escolas dos pitagóricos se assemelhavam mais a uma seita, porque elas não apenas compartilhavam conhecimento.
Os alunos, homens e mulheres, levavam uma vida estruturada de estudo e exercício, inspirados por uma filosofia baseada na matemática.
Os primeiros pitagóricos eram de classe média alta e politicamente ativos.
Eles formaram uma elite moral que se esforçou para aperfeiçoar sua forma física nesta vida para obter a imortalidade na próxima.
Segundo os pitagóricos, para libertar a alma e alcançar a imortalidade, o corpo mortal tinha que seguir uma rigorosa disciplina de forma a permanecer moralmente puro e livre da natureza básica.
Caso contrário, a alma reencarnaria repetidamente, ou "transmigraria", até que fosse liberada pelo mérito acumulado.
Os pitagóricos também acreditavam no cosmos, que na época se referia a uma ideia de perfeita ordem e beleza em todo o Universo.
Embora eles provavelmente acreditassem no politeísmo grego clássico, manifestavam fé em uma divindade superior, que estava acima de todas as outras.
Eles tinham uma série de tabus, que incluíam carne e feijão, e viviam de acordo com uma série de regras que governavam todos os aspectos da vida.
 GETTY IMAGES
GETTY IMAGESTriângulos e quadrados
Outra coisa é certa: quando falamos de Pitágoras, pensamos imediatamente nas relações entre os lados dos triângulos retângulos, descoberta que aludia a egípcios e babilônios.
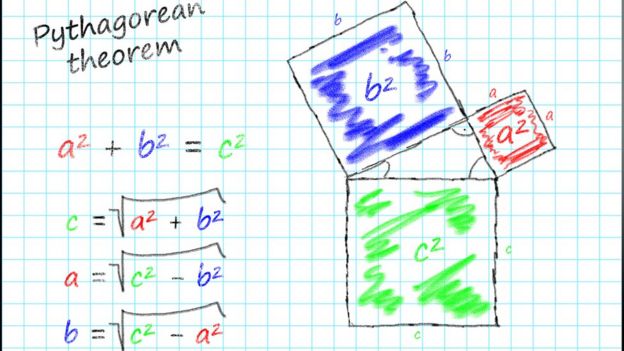
O teorema de Pitágoras afirma que, se você pegar um triângulo retângulo e fizer quadrados em todos os lados, a área do maior quadrado será igual à soma dos quadrados dos dois lados menores.
Em outras palavras, a soma dos quadrados dos catetos corresponde ao quadrado da hipotenusa.
É um teorema que ilustra uma das características da matemática grega: em vez de depender apenas de números, apela-se à geometria.
 GETTY IMAGES
GETTY IMAGESMúsica
Embora muitas descobertas que foram creditadas a Pitágoras tenham sido contestadas, existe uma teoria matemática que ainda lhe é atribuída e que tem a ver com a música.
Dizem que, ao passar por um ferreiro um dia, Pitágoras ouviu as notas produzidas pelos golpes nas bigornas e notou que elas soavam em perfeita harmonia.
Ao buscar uma explicação racional para entender essa melodia, ele recorreu à matemática e descobriu que os intervalos entre as notas musicais harmoniosas sempre apareciam em proporções de números inteiros.
Pitágoras teria ficado tão entusiasmado com a descoberta que chegou à conclusão de que todo o Universo havia sido construído a partir de números.
 GETTY IMAGES
GETTY IMAGES'Tudo é um número'
Sua doutrina de que "todas as coisas são números" era importante para a história da filosofia e da ciência.
Segundo ele, a essência e a estrutura de todas as coisas podem ser determinadas encontrando as relações numéricas que as expressam.
Originalmente, era uma ampla generalização baseada em observações como:
- que as mesmas harmonias podem ser produzidas com instrumentos diferentes por meio das mesmas relações numéricas -1: 2, 2: 3, 3: 4 - em extensões unidimensionais;
- que há certas regularidades nos movimentos dos corpos celestes;
- que a forma de um triângulo é determinada pela razão dos comprimentos de seus lados.
Mas os seguidores de Pitágoras tentaram aplicar seus princípios em todos os lugares com maior precisão.
Nessa tentativa, eles se depararam com um desafio, que emergiu de suas próprias fileiras e envolveu o teorema de Pitágoras.
 GETTY IMAGES
GETTY IMAGESA ameaça
Um dos membros de maior prestígio da Escola Pitagórica era precisamente Hipaso (que morreu afogado no Mar Mediterrâneo no início dessa reportagem).
Sem qualquer má intenção, Hipaso se lançou a encontrar o comprimento da diagonal de um triângulo retângulo com dois lados que medem uma unidade.
Talvez seja mais fácil entender dessa forma: imagine um quadrado em que cada um dos lados tem 1 unidade de comprimento.
Quanto mede a diagonal do quadrado?
Graças ao teorema de Pitágoras, podemos calcular o quadrado do comprimento do lado mais longo de um triângulo retângulo, acrescentando os quadrados dos outros dois lados.
Então o comprimento da diagonal ao quadrado é (1 × 1) + (1 × 1) = 2. Assim, o comprimento da diagonal é √2. Ou seja, o número que multiplicado por ele próprio totaliza 2.
Mas qual é esse número?
A raiz quadrada de 2 não é 1 porque 1 x 1 é 1.
E não é 2, porque 2 x 2 é 4.
É algo entre os dois.
Algo que os babilônios haviam registrado na tábua de Yale, embora não o tivessem entendido.
Tratava-se de um número irracional, (como π, o número de Euler e o número de ouro ou phi).
 GETTY IMAGES
GETTY IMAGES
Foi uma das descobertas mais fundamentais na história da ciência: o lado e a diagonal de figuras simples, como o quadrado e o pentágono regular não podem ser medidos, ou seja, a relação quantitativa não pode ser expressa por uma razão de números inteiros.
O segredo
Esses números irracionais não se encaixavam na cosmovisão pitagórica.
Além disso, a descoberta ameaçou destruir a própria base da filosofia de Pitágoras.
Basicamente, a revelação implicava que os seguidores do famoso filósofo e matemático não eram mais possuidores de uma verdade: o dogma de que tudo tem sua medida era falso e o poder que havia sido atribuído aos números também.
Se os números naturais, que para os pitagóricos constituíam a essência da realidade, nem sempre servissem para encontrar a medida das coisas, tampouco eram o meio de conquistar o conhecimento divino.

Especialistas da Grécia Antiga contam que Pitágoras fez sua escola jurar que não revelaria a descoberta.
No entanto, Hipaso insistiu em divulgar a natureza do comensurável e imensurável, o conhecimento dos números irracionais "perigosos".
Esse teria sido o motivo do suposto crime: silenciá-lo.
Provavelmente, nunca saberemos se esse foi realmente o fim da história de Hipaso de Metaponto.
O que sabemos é que, apesar disso, os números irracionais acabaram vindo à tona.

Comentários
Postar um comentário